프로젝트 오일러 009
세 변의 길이가 모두 자연수이고 그 합이 1,000인 직각삼각형 찾기

문제

세 변이 각각 자연수이며, 그 둘레의 합이 1,000인 직각삼각형의 변의 길이들의 곱을 구하는 문제입니다. 간단한 문제처럼 보이지만, 1부터 999 사이의 범위에 변의 길이가 있다고 가정하고 두 조건을 만족하는 수의 삼조(triple)를 찾으려고 해도 검사해야 하는 대상이 1억 6천만이 넘습니다. 물론 문제에서는 조건을 만족하는 조합이 1개만 존재한다는 엄청난 힌트를 주었기 때문에, 1억 6천만 가지 조합을 모두 검사할 필요는 없겠습니다만, 최악의 케이스에는 그렇게 해야할 수도 있겠죠.
피타고라스 삼조
피타고라스 성질을 만족하는 세 개의 정수 (a, b, c)를 피타고라스 삼조라고 합니다. 피타고라스 삼조의 배수들도 피타고라스 삼조입니다. 각 성분이 서로 소인 피타고라스 삼조를 원시 피타고라스 삼조라고 하는데, 원시 피타고라스 삼조는 서로 소인 두 정수 m, n 이 있으면 얼마든지 만들어 낼 수 있습니다.
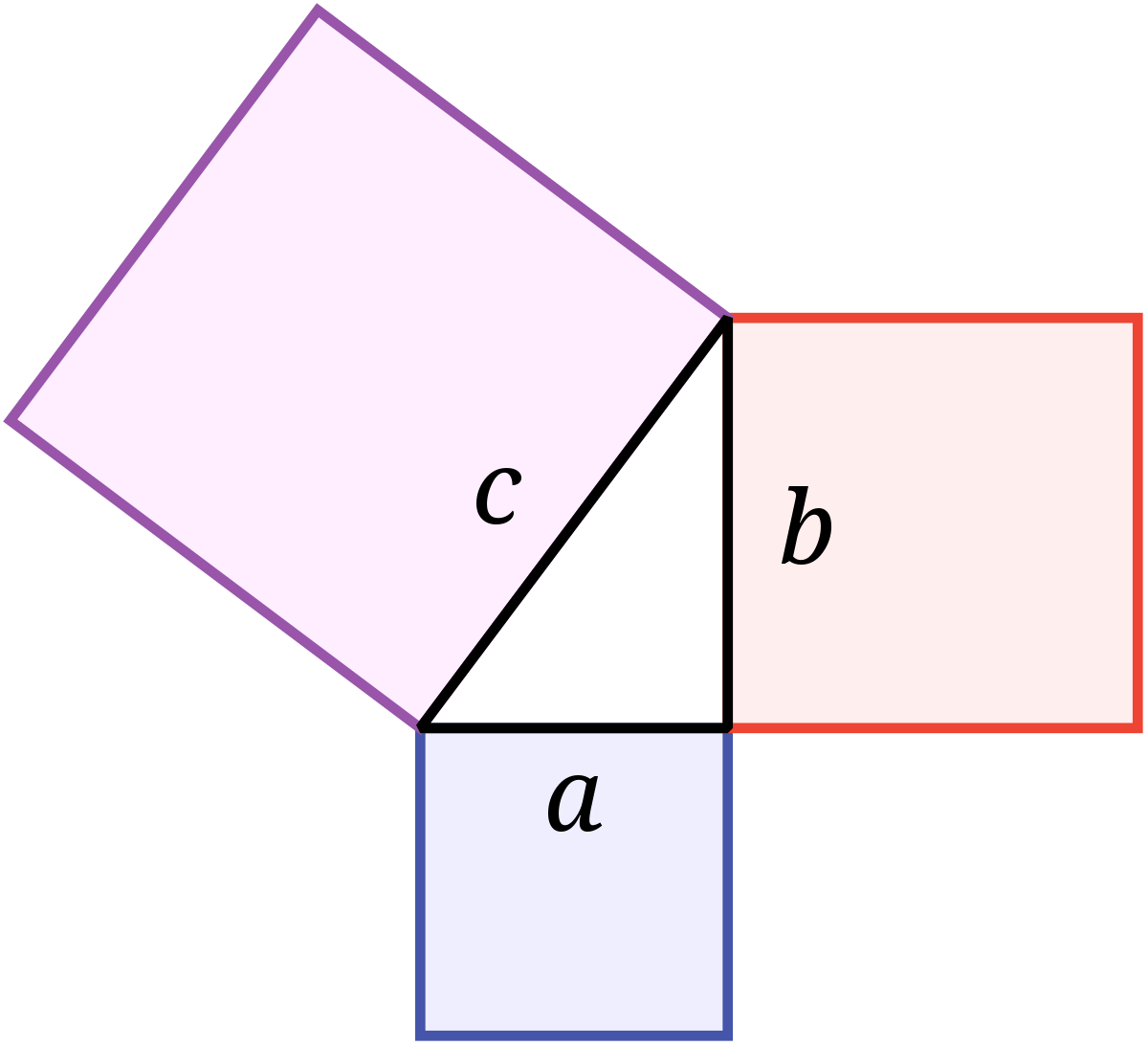
이 성질을 사용하여 피타고라스 삼조를 만들고, 그 합이 1000의 약수라면, 그 피타고라스 삼조의 배수 중에서 답을 찾으면 됩니다.
def gcd(a, b):
if a < b:
return gcd(b, a)
while True:
_, r = divmod(a, b)
if r == 0:
return b
a, b = b, r
def main():
for m in range(2, limit):
for n in range(1, m):
if gcd(m, n) == 1:
a = m * m - n * n
b = 2 * m * n
c = m * m + n * n
s = a + b + c
q, r = divmod(1000, s)
if r == 0:
print(f"{s=}, {a=}, {b=}, {c=}, {m=}, {n=}")
print( a * b * c * q ** 3)
main()
범위를 줄이기
그런데 피타고라스 삼조는 교과과정에 (요즘은 나오는지도 모르겠습니다만!) 나오지 않는 것 같아서 좀 반칙스러운 면이 있습니다. 그러면 중고등학교 수준에서의 삼각형의 변의 길이에 대한 성질들로부터 반복 횟수를 줄일 수 있을만한 힌트가 있는지 살펴보겠습니다.
둘레의 길이를 P=1000으로 하고, 조건을 만족하는 직각 삼각형의 세 변의 길이를 각각 a < b < c 라고 둡니다.
- 직각 이등변 삼각형의 빗변은 다른 변의 길이의 루트2배이기 때문에 정수가 될 수 없습니다. 따라서 a < b 여야 합니다.
- a < b 이기 때문에 a는 P / 3 보다는 작아야 합니다.
- c = P - a - b 이며, c < a + b 여야 합니다. 따라서 b의 범위는 a < b < (P - a) / 2 + 1 사이에 오게됩니다.
a와 b의 범위를 한정하는 것만으로도 전수 검사의 범위가 크게 줄어듭니다.
def solve009():
p = 1000
for a in range(1, p // 3 + 1):
for b in range(a + 1, (p - a) // 2 + 1):
c = p - a - b
if c * c == a * a + b * b:
print(a * b * c)
return
물론 피타고라스 삼조를 이용해서 찾은 풀이보다는 몇 십배 느리지만, 이 역시 0.01초 이내에 답을 구할 수 있습니다.



